Frozen
Here is an active version
Trilobite: a System of Game Rules and AI
The game, described earlier and which was almost alive is not yet clever. Let’s try to add a bit of intelligence to it.
Game Rules Engine
Since we can calculate all combinations (for the time being for a tiny board), the rule engine will simply be a tree-like structure of data1.
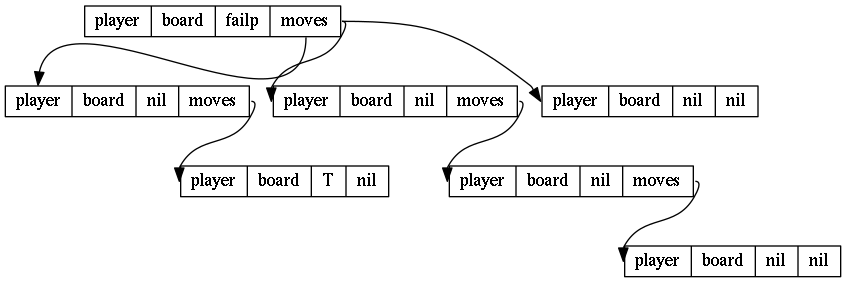
;; game rules engine is a tree which elements are lists
(defstruct (game-node (:type list))
player ; *human-player* or *ai-player*
board ; current board situation
failp ; is it a fail?
moves) ; nil or list of lists (move cell . game-tree).
| Field | Type | Purpose |
|---|---|---|
| player | number | player who will make move now |
| board | array | board |
| failp | flag | current player lost |
| moves | list of elements (cell . node) | the cell where the current player place the chip to and the node of the tree |
The rule engine will check the admissibility of moves for a player, provide artificial intelligence with the necessary data and detect victory/defeat. The leaves of the engine tree are the nodes with the flag of defeat or an empty list of possible moves, the latter means a draw.
So we create the rules engine tree, this is done by one recursive function, and it perfectly copes with the tiny 3x3 board, but it quickly exhausts the stack and breaks down on large boards.
;; new tree
(defun game-tree (board player move)
(let ((fail (if (eql -1 move)
nil
(test-for-win board move
(change-player player)))))
(make-game-node
:player player
:board board
:failp fail
:moves
(if fail
'()
(mapcar (lambda (move)
(list move
(game-tree (board-add-move board move player)
(change-player
player)
move)))
(possible-moves board))))))
The parameter move for this function means the cell where the move was made, which led to this situation on the board. If move is -1, then it means that there was no previous move - this is the most initial combination and it is not necessary to check if someone has lost.
First of all, we check to see if anyone has lost, in this case it is a leaf combination on the board and we do not build any further combinations. Otherwise, we build the nodes of the tree for all possible moves on the given board.
AI
Artificial intelligence will be a simple implementation of the minimax algorithm. Its essence lies in the fact that in predicting the development of the game situation AI behaves as follows:
- AI always chooses the move with the maximum score;
- AI believes that a player chooses a move with a minimum score..
In other words AI calculates that the player will act the worst for the AI way.
Scores, here a draw is better than a loss, but worse than a victory:
(defparameter *ai-win* 1)
(defparameter *draw* 0)
(defparameter *human-win* -1)
The following two functions implement this algorithm.
(defun rate-position (tree)
(let ((moves (game-node-moves tree)))
(if moves
(apply (if (eq *ai-player* (game-node-player tree))
#'max
#'min)
(get-ratings tree))
(if (game-node-failp tree)
(if (eql *ai-player* (game-node-player tree))
*human-win*
*ai-win*)
*draw*))))
(defun get-ratings (tree)
(mapcar (lambda (move)
(rate-position (cadr move)))
(game-node-moves tree)))
Let’s check how the calculation of scores for moves works. Create an empty board where AI will be the first to go, remember it for convenience in the variable *game* and see how it evaluates its possible moves:
* (defvar *game* (game-tree (new-board) *ai-player* -1))
*GAME*
* (game-node-board *game*) ; look at the board
#(0 0 0 0 0 0 0 0 0)
* (get-ratings *game*) ; let's see the scores
(0 0 0)
It seems that the computer does not care where to go - all moves are estimated as leading to a draw. Let’s see what happens if we simulate the choice of AI of the first move.
To do this, extract the second element of the first move (cadar list-moves) and remember it in the variable *first-move*:
* (defvar *first-move* (cadar (game-node-moves *game*)))
*FIRST-MOVE*
Let’s check the scores of the situation:
* (game-node-board *first-move*)
#(0 0 0 0 0 0 1 0 0)
* (get-ratings *first-move*)
(1 1 0)
Aha! The computer saw for itself two possible ways to victory! It’s unlikely that he will be able to use them, because now the turn of player, and he certainly chooses the last move, which leads to a possible draw.
Let’s formulate the actions of the computer as a function:
; ai
(defun handle-computer (tree)
(let ((ratings (get-ratings tree)))
(cadr (nth (position (apply #'max ratings) ratings) (game-node-moves tree)))))
Here in two lines next is written: when the computer is given the opportunity to make a move, it calculates the scores for possible moves and chooses the move with the maximum score.
Let’s see what move AI chooses at the very beginning, when all the moves lead to a possible draw:
* (defvar *game* (game-tree (new-board) *ai-player* -1))
*GAME*
* (game-node-board (handle-computer *game*))
#(0 0 0 0 0 0 1 0 0)
-
Made with a small program for Graphviz. ↩

