Yellow Rabbit

Старая версия

Здесь находится настоящий сайт

Акселерометр Android и фильтр нижних частот

06 Aug 2017 • 3 мин. читать • Comments •

Фильтр нижних частот для датчиков Android

Разнообразные датчики в наших мобильных телефонах объединяет, кроме всего прочего, неидеальное качество выходного сигнала. Ну с аппаратной частью что-нибудь сделать затруднительно, но можно поиграться с программными цифровыми фильтрами сигналов.

Немного теории

Рассмотрим простеёший фильтр нижних частот: Принципиальная схема RC фильтра

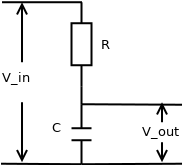
Падение напряжения на резисторе и ток через него связаны:

С другой стороны из определения ёмкости следует:

Где \(Q_c(t)\) - заряд конденсатора в момент времени \(t\). Отсюда \(i(t)=C\frac{V_{out}(t)}{dt}\) и окончательно фильтр описывается уравнением:

Можно перейти к дискретной форме. Допустим, что входной и выходной сигналы снимаются через равные промежутки времени \( \Delta T\), последовательность \(\lbrace x_1, x_2, x_3, \ldots x_n\rbrace\) - входной сигнал \(V_{in}\), \(\lbrace y_1, y_2, y_3, \ldots y_n\rbrace\) - выходной \(V_{out}\), тогда:

или

\(\alpha=\frac{RC}{RC+\Delta T}\) - коэффициент сглаживания. Из \(RC\) определяется частота сглаживания фильтра \(f_c=\frac{1}{2\pi RC}\), то есть частота, выше которой сигнал начинает сглаживаться.

Фильтр на Maxima

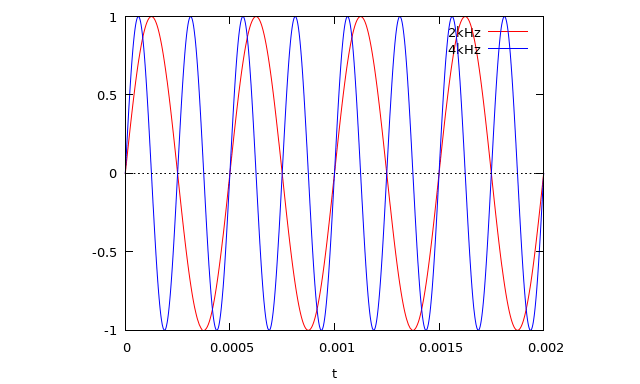
Допустим у нас есть на входе полезный сигнал с частотой 2кГц и шум с частотой 4кГц:

Входной сигнал и шум

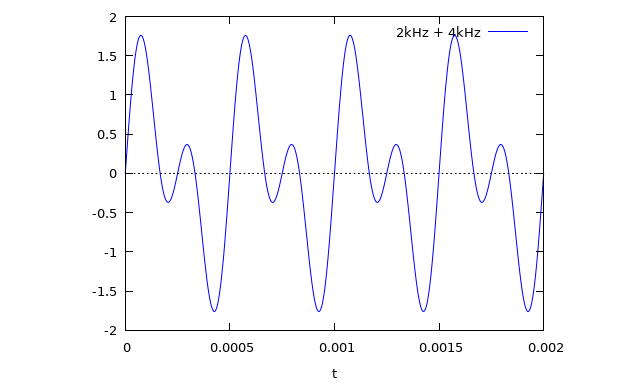
Естественно на вход фильтра поступает суммарный сигнал:

Суммарный входной сигнал

Сигнал и шум задаём функциями:


kH2(t):=sin(2*%pi*2000*t)$
kH4(t):=sin(2*%pi*4000*t)$

В Maxima мы можем описать входные данные двумя списками значений, tl - отсчёты времени 100 интервалов по 0.00005 секунды, kH2lkH4l - список входных значений \(x_i\):

tl:makelist(i / (100 * 500), i, 0, 100)$
kH2lkH4l:makelist(kH4(i / (100 * 500)) + kH2(i / (100 * 500)), i, 0, 100)$

Сама функция фильтра состоит из рекурсивной части, которая дословно повторяет \(y_i=\alpha y_{i-1} + (1 - \alpha)x_i\):


lowpass_rec(x, alpha):= 
  if length(x) = 1 then
    [(1 - alpha) * first(x)]
  else block([y],
    y: lowpass_rec(rest(x), alpha),
    return(cons(alpha * first(y) + (1 - alpha) * first(x), y)))$

и точки входа:


lowpass(x, alpha):=reverse(lowpass_rec(reverse(x), alpha))$

\(\Delta T=0.00005\) у нас фиксирована и определяется частотой поступления данных от датчика. Частоту сглаживания возьмём 3кГц: \(f_c=\frac{1}{2\pi RC}=3000\)Гц.

Посмотрим как работает фильтр с этим значением \(\alpha\) вместе с другими.


plot2d([[discrete, tl, kH2lkH4l], [discrete, tl, lowpass(kH2lkH4l, 0.5)],
        [discrete, tl, lowpass(kH2lkH4l, 0.7262210965743948)],
        [discrete, tl, lowpass(kH2lkH4l, 0.9)]],
        [legend, "V_in", "a=0.5", "a=0.726", "a=0.9"])$

Работа фильтра нижних частот

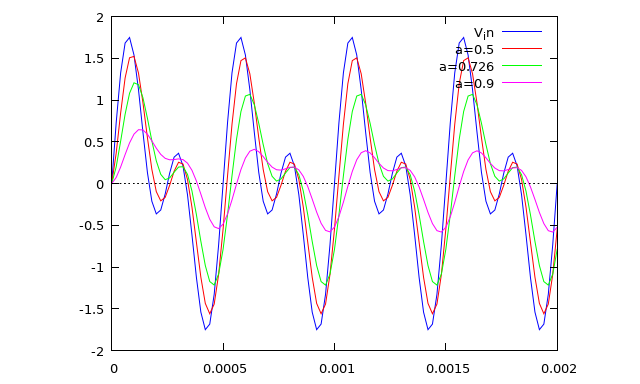
Для остальных приведённых значений \(\alpha\) граничные частоты данного фильтра равны соответственно:

Гц - через фильтр проходит всё практически без изменений.

Гц - фильтр активно сглаживает и наш сигнал в 2кГц и шум в 4кГц.

Послесловие

Кажется, что уже можно вставить этот фильтр как есть куда-нибудь вроде:


  @Override
    public void onSensorChanged(SensorEvent event)
    {

\(\ldots\) и разочароваться. Дело в \(\Delta T\) или в периоде дискретизации, которое изменяется от модели к модели, да и во время работы программы может варьироваться довольно значительно. И при фиксированной \(\alpha\) это приведёт к изменению рабочей частоты фильтра. Так что \(\alpha\) должна быть динамической, но этом в следующий раз. :smile: