Yellow Rabbit

Старая версия

Здесь находится настоящий сайт

Фильтр нижних частот на практике

07 Aug 2017 • 5 мин. читать • Comments •

Фильтр нижних частот для датчиков Андроид - практика

Как было обещано для учёта разброса частоты получения данных с датчиков устройств на Android переходим от статического коэффициента сглаживания к динамическому.

Динамический коэффициент сглаживания

Сырые данные накапливаем в rawAccData, обработанные фильтром - в lpfAccData. Переменные count и beginTime нужны для вычисления среднего периода дискретизации. В этой простой программе датчики опрашиваются постоянно поэтому эти переменные можно инициализировать при запуске. В реальных программах нужно учитывать останов опроса на время паузы и т.д.


    private final int MAX_TESTS_NUM = 200 * 60; // одна  минута измерений с частотой 200Гц
    private final float[] rawAccData = new float[MAX_TESTS_NUM * 3];
    private int rawAccDataIdx = 0;

    // ФНЧ
    private final float[] lpfAccData = new float[MAX_TESTS_NUM * 3];
    private final float[] lpfPrevData = new float[3];
    private int count = 0;
    private float beginTime = System.nanoTime();
    private float rc = 0.002f;

Где-то в обработчике событий от датчиков пропишем вызов чтения данных:


    public void onSensorChanged(SensorEvent event) {
        // ...
            readSensorData(event);
        // ...

Считываем данные и применяем фильтр:


    private void readSensorData(SensorEvent event) {
        final int type = event.sensor.getType();
        if (type == Sensor.TYPE_ACCELEROMETER) {
            System.arraycopy(event.values, 0, rawAccData, rawAccDataIdx, 3);
            applyLPF();
            rawAccDataIdx += 3;
            if (rawAccDataIdx >= rawAccData.length) {
                stopMeasure();
            }
        }
    }

Собственно сам фильтр: вычисляем средний период дискретизации, определяем \(\alpha\) и используем формулу:


    private void applyLPF() {
        final float tm = System.nanoTime();
        final float dt = ((tm - beginTime) / 1000000000.0f) / count;

        final float alpha = rc / (rc + dt);

        if (count == 0) {
            lpfPrevData[0] = (1 - alpha) * rawAccData[rawAccDataIdx];
            lpfPrevData[1] = (1 - alpha) * rawAccData[rawAccDataIdx + 1];
            lpfPrevData[2] = (1 - alpha) * rawAccData[rawAccDataIdx + 2];
        } else {
            lpfPrevData[0] = alpha * lpfPrevData[0] + (1 - alpha) * rawAccData[rawAccDataIdx];
            lpfPrevData[1] = alpha * lpfPrevData[1] + (1 - alpha) * rawAccData[rawAccDataIdx + 1];
            lpfPrevData[2] = alpha * lpfPrevData[2] + (1 - alpha) * rawAccData[rawAccDataIdx + 2];
        }
        if (isStarted) {
            lpfAccData[rawAccDataIdx]     = lpfPrevData[0];
            lpfAccData[rawAccDataIdx + 1] = lpfPrevData[1];
            lpfAccData[rawAccDataIdx + 2] = lpfPrevData[2];
        }
        ++count;
    }

Практика

Попробуем применить этот фильтр для выделения линейных ускорений из сигналов акселерометра путем избавления от гравитационной составляющей.

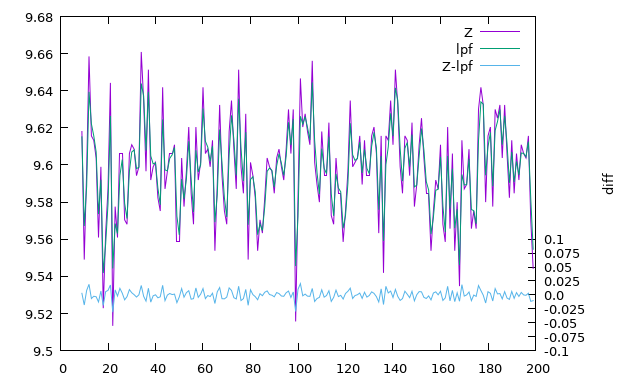
Неподвижный телефон, \(RC=0.002\):

График сырых данных, фильтра и разницы при rc=0.002 и неподвижном телефоне

Неподвижный телефон под углом, \(RC=0.002\):

График сырых данных, фильтра и разницы при rc=0.002 и наклоненном телефоне

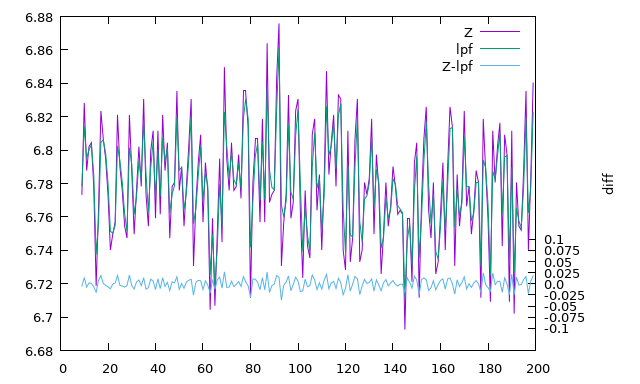
Кажется, что нам удалось очень эффективно избавиться от гравитационной составляющей. И это неудивительно: при \(RC=0.002\) частота среза фильтра будет \(f_c=79.577471\)Гц и значит, что через фильтр пройдёт фактически всё, и мы по сути вычитаем из входного сигнала его же.

Это не очень подходит для выделения линейных ускорений.

Настраиваем частоту среза

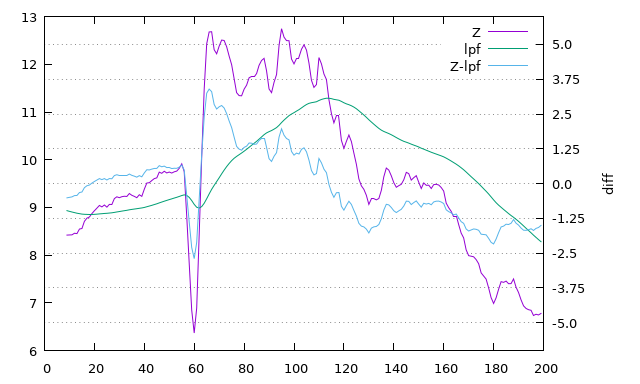
Возьмём \(RC=0.18\), тогда частота среза будет \(f_c=0.884194\)Гц, а это уже отфильтрует значительное количество верхних частот.

Теперь двигаем и наклоняем телефон:

График при rc=0.18 и двигающимся телефоне

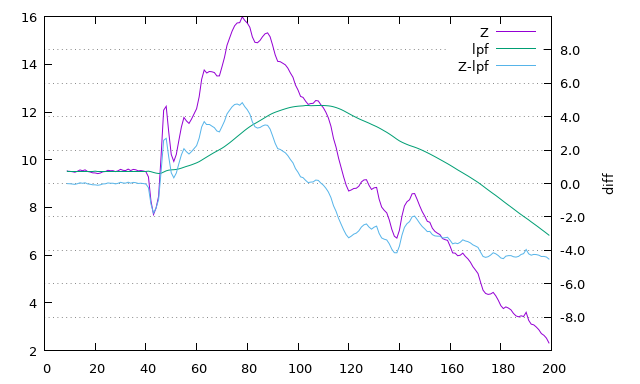
При \(RC=0.288731\) и частоте среза соответственно \(f_c=0.551222\) Гц:

График при rc=0.288731 и двигающимся телефоне

Заключение

Используя фильтр нижних частот для выделения гравитационной составляющей в показаниях акселерометра Android оправдано лишь на коротких промежутках времени.